Van egy ember, a nemrég elhunyt Dr. Albert Bartlett aki valami annyira triviális, mégis alapvető dologra hívta fel a figyelmet, hogy kézenfekvő vele kezdeni a retrospektív szekciót. Ha valami annyira fontos volt számára, hogy képes volt az 'Aritmetika, populáció és energia' című előadását 36 éven át egészen pontosan 1742 alkalommal megtartani, talán érdemes odafigyelni rá. Dr. Bartlett az előadásait mindig a következő állítással kezdte: "Az emberi faj legnagyobb hiányossága, hogy nem vagyunk képesek megérteni az exponenciális függvényt".

Aritmetika

A függvény értelmezése egyébként nem igényel egyetemi diplomát, ha jól emlékszem középiskolai tananyag. Nagyon pongyolán fogalmazva minden növekedés exponenciális, ami időegység alatt adott százalékkal konstans mértékben változik. Ha tehát időegység alatt valami 5%-kal növekszik, következik belőle, hogy a 100%-os növekedéshez, azaz adott helyiérték megduplázásához ennek az időnek valamilyen többszöröse szükséges. Ezt nevezik duplázódási (csökkenő függvénynél felezési)időnek. Ez egy egyszerű művelettel kiszámítható, de hogy ne veszítsem el ezen a ponton az olvasók egy részét, maradjunk annyiban, hogy a duplázódás ideje kb. megadható, ha 70-et osztjuk el a növekedés mértékével. Ha valakit a képletek is érdekelnek itt tessék utánajárni, illetve a lenti videót is ajánlom, ha van szabad egy órád, és angol nyelvtudásod. Egyszerű példával szemléltetve, ha az időegységünk az év, és adott évben a függvény értéke 100, 5%-os éves szintű növekedés esetén 70/5 = 14 év alatt fogja elérni értéke a 200-at.

A klasszikus példa, amit Bartlett is említ előadásában az exponenciális növekedésre a sakk feltalálásához kapcsolódó anekdota. A történet szerint a feltaláló nem kért fizetséget a királytól, akinek eladta, csupán annyit, hogy az első mezőre tegyenek egy búzaszemet, a következőre kettőt, majd minden mezőre az azt megelőző dupláját.Így, mire a 64. mezőre érünk ott már 2^63 búzaszemet kellene elhelyezni. Hogy összesen ez mennyi búzaszemet jelent? Bartlett becslése szerint a világ 1990-es búzatermésének kb. 400 szorosa. 

Az exponenciális növekedésnek van még egy említésre méltó tulajdonsága: ha megfigyeljük a sakktáblára kerülő búzaszemeket, megállapítható, hogy minden új mezőre több szem kerül, mint az addigi összes mező összes búzaszeme. 2^n búzaszem esetén 2^n+1 -1 a teljes összeg a sakktáblán. Szó szerint beláthatatlan következményei vannak az exponenciális függvénynek az életünkre és bolygónk jövőjére, ha a népesség vagy a nyersanyag-felhasználás problémájára gondolunk.

Népességnövekedés

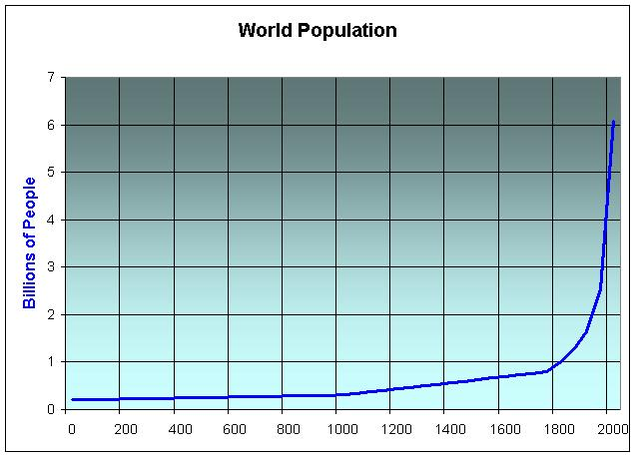
A világ népessége 1986-ban érte el az 5 milliárd főt, és az akkori híradások szerint 1,7%-os volt a növekedés üteme. Habár ez a növekedési ütem kicsinek hat, kiszámítható, hogy a hozzá tartozó duplázódási idő 41 év. 1999-ben a föld népessége elérte a 6 milliárd főt, a növekedés üteme szerencsésen csökkent, immáron mindössze 1,3%, 53 éves duplázódási idővel. Ez éves szintre vetítve 80 millió főt ad hozzá a világ népességéhez. Ha ezzel az értékkel számolunk tovább, Bartlett előrevetíti, hogy a szárazföldi területek minden egyes négyzetméterére jutni fog egy ember 780 év múltán, és 2400 év alatt az emberiség össztömege eléri a Földét. Ez persze nyilvánvaló nonszensz. Teljesen világos, hogy a növekedés üteme fenntarthatatlan, és előbb-utóbb szükségszerűen csökkenni kezd a népesség. A probléma ezzel mindössze az, hogy minden olyan behatás, ami eredményesen csökkentené a populációt morálisan és társadalmilag elfogadhatatlan számunkra. A kérdés ugyanakkor fennáll, mégis hány évig növekedhet még a föld népessége? Valahol, valamikor bele kell ütköznünk a bolygó szabta határokba. 

A véges környezetben történő exponenciális növekedés problémáját baktériumok osztódásával szokás szemléltetni. Tegyük fel, hogy egy zárt üvegben, megfelelő ellátás mellett baktériumok kezdenek osztódni. A duplázódási idejük egy perc, és 11:00-kor az üveget üres, 12:00-kor teljesen telített állapotúnak érzékeljük. Mikor van félig az üveg? A duplázódási idő miatt csak 11:59-re érik el. Vajon az egyes baktérium szintjén mikor realizálódik, hogy kifutnak a szabad térből? 11:55-kor bármilyen meglepő még mindössze 3,1% az üveg telítettsége.

Ez az alapvető dilemmája az exponenciális növekedésnek. A földi erőforrások 3%-os kihasználtságakor vajon hányunk érzékelné, hogy bármiféle probléma lehet?

A nem-megújuló erőforrások természete

A témakörben kötelező kűr elsőként megemlíteni M. King Hubbert geológusprofesszor nevét. Legismertebb kutatásai a kőolaj- és földgázmezők kapacitásbecsléséhez kapcsolódnak. Előrejelzései alapján bármely adott földrajzi területet tekintve, az egyes olajmezőktől a teljes bolygóig, a kőolaj-kitermelés időbeli változása egy haranggörbére emlékeztető görbét, a logisztikus eloszlás görbéjét fogja követni. Az erre az elméletre alapuló cikkét 1956-ban tette közzé. Ebben azt jósolta, hogy az Amerikai Egyesült Államok teljes kőolajtermelése az 1960-as évek vége és az 1970-es évek eleje között fog tetőzni. Jóslata 1970-ben valóra is vált. A modelljében használt görbe Hubbert-görbeként, csúcsa pedig Hubbert-csúcsként, illetve általános formában olajhozamcsúcsként ismert, mondja a Wikipédia. 

Hogy értsük, miről van szó, visszacsatolva az aritmetikára: a kőolaj kitermelése ugyebár növekszik a 20. század során, és tette ezt Amerikában is 1970 előtt. A korábbiak alapján kézenfekvő, hogy az évenkénti rendszeres növekedéssel (az alábbi videóból kiderül, ha jól emlékszem 7%) együtt jár egy duplázódási idő. Ha a 7%-os adattal számolunk ez azt jelenti, hogy a világ kb. 10 évente megduplázza a korábbi kitermelését. A geológia és fizika szabályai azonban közbeszólnak, és nem teszik lehetővé, hogy a kőolaj kitermelés volumenét egészen az utolsó cseppig növeljük. Az egyes kutak, és így a kőolajmezők, illetve áttételesen a teljes világ olajhozama az élettartama feléhez érve volumenében tetőzik, majd különböző mértékű csökkenésbe kezd.

Így tehát, ahogy mindig nagyon fontos hangsúlyozni a laikusok számára, az olajhozam csúcs nem azt jelenti, hogy elfogy a kőolajunk, hanem éppen azt, hogy a készleteink kb. feléhez érkeztünk. A problémát itt az jelenti, hogy a világ energiafelhasználása, és gazdasági növekedése számos áttéten keresztül közvetlenül hat egymásra, és míg a fosszilis energiahordozókra érvényesek a fizika törvényei, addig a GDP növekedésre nem. Ez számos megoldandó problémát vetít előre, és rajzol szürke esőfelhőket reménybeli jövőnk fényes, kék egére. Értsd: hogyan lehet fenntartani a növekedést, ha annak legalapvetőbb motorja, az energiatermelés nem tud lépést tartani vele.

Természetesen ez az egész most csak röviden, konyhanyelven összefoglalva, jogosan jöhetnének a kérdések, hogy akkor miért tudjuk még mindig növelni a kőolaj kitermelés nettó volumenét. (Egyébként nem tudjuk, a hagyományos kőolaj kitermelése 2005-ben tetőzött, és azóta csökkenést mutat, de ezt egy huszárvágással megoldva ma már minden kőolajszármazékot beleszámít az IEA, de erről a későbbiekben még épp elég szó fog esni.)